En vez de estimar el valor de un parámetro, a veces se debe decidir si una afirmación relativa a un parámetro es verdadera o falsa. Es decir, probar una hipótesis relativa a un parámetro. Se realiza una prueba de hipótesis cuando se desea probar una afirmación realizada acerca de un parámetro o parámetros de una población.
Una hipótesis es un enunciado acerca del valor de un parámetro (media, proporción, etc.).
Prueba de Hipótesis es un procedimiento basado en evidencia muestral (estadístico) y en la teoría de probabilidad (distribución muestral del estadístico) para determinar si una hipótesis es razonable y no debe rechazarse, o si es irrazonable y debe ser rechazada.
La hipótesis de que el parámetro de la población es igual a un valor determinado se conoce como hipótesis nula. Una hipótesis nula es siempre una de status quo o de no diferencia.

En toda prueba de hipótesis se presentan 3 casos de zonas críticas o llamadas también zonas de rechazo de la hipótesis nula, estos casos son los siguientes:
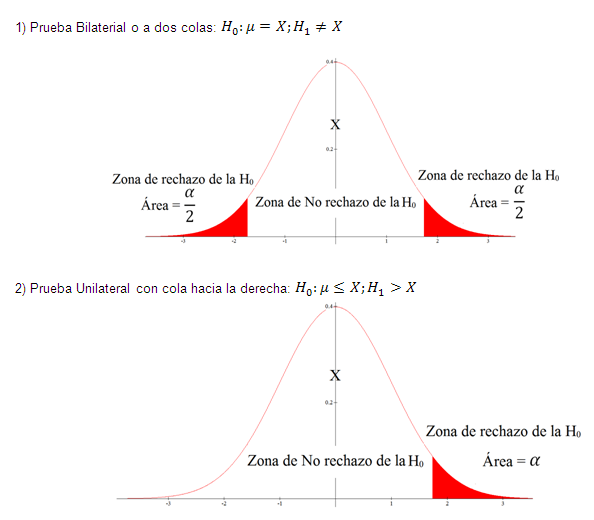

En toda prueba de hipótesis se pueden cometer 2 tipos de errores:
