prueba de hipotesis

http://www.geociencias.unam.mx/~ramon/EstInf/Clase13.pdf

prueba de hipotesis para la media ,varianza y proporcion

En vez de estimar el valor de un parámetro, a veces se debe decidir si una afirmación relativa a un parámetro es verdadera o falsa. Es decir, probar una hipótesis relativa a un parámetro. Se realiza una prueba de hipótesis cuando se desea probar una afirmación realizada acerca de un parámetro o parámetros de una población.

Una hipótesis es un enunciado acerca del valor de un parámetro (media, proporción, etc.).

Prueba de Hipótesis es un procedimiento basado en evidencia muestral (estadístico) y en la teoría de probabilidad (distribución muestral del estadístico) para determinar si una hipótesis es razonable y no debe rechazarse, o si es irrazonable y debe ser rechazada.

La hipótesis de que el parámetro de la población es igual a un valor determinado se conoce como hipótesis nula. Una hipótesis nula es siempre una de status quo o de no diferencia.

En toda prueba de hipótesis se presentan 3 casos de zonas críticas o llamadas también zonas de rechazo de la hipótesis nula, estos casos son los siguientes:

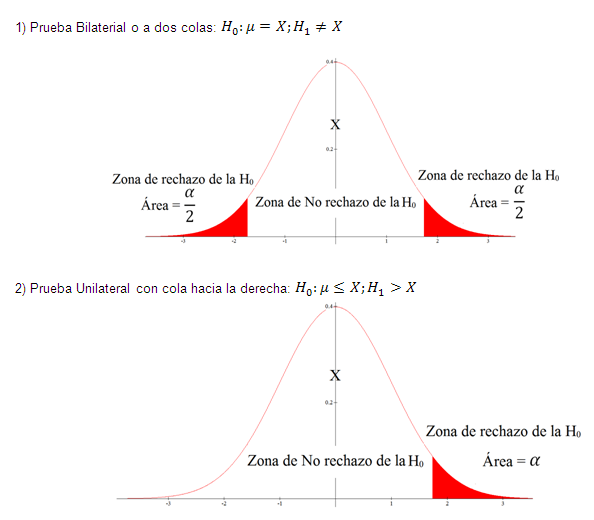
En toda prueba de hipótesis se pueden cometer 2 tipos de errores:

intervalo de confianza para la varianza

Intervalo de confianza para la varianza de una distribución Normal

Dada una variable aleatoria con distribución Normal N(μ; σ), el objetivo es la construcción de un intervalo de confianza para el parámetro σ, basado en una muestra de tamaño n de la variable.  A partir del estadístico la fórmula para el intervalo de confianza, con nivel de confianza 1 − α es la siguiente Donde χ2α/2 es el valor de una distribución ji-cuadrado con n − 1 grados de libertad que deja a su derecha una probabilidad de α/2. Por ejemplo, dados los datos siguientes: Distribución poblacional: Normal Tamaño de muestra: 10 Confianza deseada para el intervalo: 95 % Varianza muestral corregida: 38,5 Un intervalo de confianza al 95 % para la varianza de la distribución viene dado por: que resulta, finalmente

estimadores

ESTIMADORES Y PARÁMETROS.

En una población cuya distribución es conocida pero desconocemos algún parámetro, podemos estimar dicho parámetro a partir de una muestra representativa.

Un  estimador  es un valor que puede calcularse a partir de los datos muéstrales y que proporciona información sobre el valor del parámetro. Por ejemplo la media muestral es un estimador de la media poblacional, la proporción observada en la muestra es un estimador de la proporción en la población.

Una estimación es puntual cuando se obtiene un sólo valor para el parámetro. Los estimadores más probables en este caso son los estadísticos obtenidos en la muestra, aunque es necesario cuantificar el riesgo que se asume al considerarlos. Recordemos que la distribución muestral indica la distribución de los valores que tomará el estimador al seleccionar distintas muestras de la población. Las dos medidas fundamentales de esta distribución son la media que indica el valor promedio del estimador y la desviación típica, también denominada error típico de estimación, que indica la desviación promedio que podemos esperar entre el estimador y el valor del parámetro.

Más útil es la estimación por intervalos en la que calculamos dos valores entre los que se encontrará el parámetro, con un nivel de confianza fijado de antemano.

Llamamos  Intervalo de confianza al intervalo que con un cierto nivel de confianza, contiene al parámetro que se está estimando.

Nivel de confianza es la "probabilidad" de que el intervalo calculado contenga al verdadero valor del parámetro. Se indica por  1-a y habitualmente se da en porcentaje (1-a)100%. Hablamos de nivel de confianza y no de probabilidad ya que una vez extraída la muestra, el intervalo de confianza contendrá al verdadero valor del parámetro o no, lo que sabemos es que si repitiésemos el proceso con muchas muestras podríamos afirmar que el (1-a)% de los intervalos así construidos contendría al verdadero valor del parámetro.

Los dos problemas fundamentales que estudia la inferencia estadística son el "Problema de la estimación" y el "Problema del contraste de hipótesis". Cuando se conoce la forma funcional de la función de distribución que sigue la variable aleatoria objeto de estudio y sólo tenemos que estimar los parámetros que la determinan, estamos en un problema de inferencia estadística paramétrica; por el contrario, cuando no se conoce la forma funcional de la distribución que sigue la variable aleatoria objeto de estudio, estamos ante un problema de inferencia estadística no paramétrica. Nosotros nos vamos a limitar a problemas de inferencia estadística paramétrica, donde la variable aleatoria objeto de estudio sigue una distribución normal, y sólo se estimarán los parámetros que la determinan, la media y la desviación típica.

Estadístico

: Son los datos o medidas que se obtienen sobre una muestra y por lo tanto una estimación de los parámetros.

Parámetro

Se llama parámetros poblacionales a cantidades que se obtienen a partir de las observaciones de la variable y sus probabilidades y que determinan perfectamente la distribución de esta, así como las características de la población, por ejemplo: La media, μ, la varianza σ

Los Parámetros poblacionales son números reales, constantes y únicos.

: Son las medidas o datos que se obtienen de la población, es decir, simplemente es el valor poblacional de las características de una población. 2, la proporción de determinados sucesos, P.

Parámetros muéstrales

Los Parámetros muéstrales son resúmenes de la información de la muestra que nos "determinan" la estructura de la muestra. Los Parámetros muéstrales no son constantes sino variables aleatorias pues sus valores dependen de la

estructura de la muestra que no es siempre la misma como consecuencia del muestreo aleatorio. A estas variables se les suele llamar estadísticos.

Los estadísticos se transforman en dos tipos: estadísticos de centralidad y estadísticos de dispersión.

EVIDENCIAS DE CURSOS MOC

T-STUDENT

DISTRIBUCION "t DE STUDENT"

Supóngase que se toma una muestra de una población normal con media  y varianza . Si es el promedio de las n observaciones que contiene la muestra aleatoria, entonces la distribución  es una distribución normal estándar. Supóngase que la varianza de la población ² es desconocida. ¿Qué sucede con la distribución de esta estadística si se reemplaza  por s? La distribución t proporciona la respuesta a esta pregunta.

La media y la varianza de la distribución t son  = 0 y  para >2, respectivamente.

La siguiente figura presenta la gráfica de varias distribuciones t. La apariencia general de la distribución t es similar a la de la distribución normal estándar: ambas son simétricas y unimodales, y el valor máximo de la ordenada se alcanza en la media  = 0. Sin embargo, la distribución t tiene colas más amplias que la normal; esto es, la probabilidad de las colas es mayor que en la distribución normal. A medida que el número de grados de libertad tiende a infinito, la forma límite de la distribución t es la distribución normal estándar.

Propiedades de las distribuciones t

1. Cada curva t tiene forma de campana con centro en 0.



2. Cada curva t, está más dispersa que la curva normal estándar z.


3. A medida que  aumenta, la dispersión de la curva t correspondiente disminuye.


4. A medida que  , la secuencia de curvas t se aproxima a la curva normal estándar, por lo que la curva z recibe a veces el nombre de curva t con gl = 

La distribución de la variable aleatoria t está dada por:

Esta se conoce como la distribución t con  grados de libertad.

Sean X₁, X₂, . . . , X_n variables aleatorias independientes que son todas normales con media  y desviación estándar . Entonces la variable aleatoria  tiene una distribución t con  = n-1 grados de libertad.

La distribución de probabilidad de t se publicó por primera vez en 1908 en un artículo de W. S. Gosset. En esa época, Gosset era empleado de una cervecería irlandesa que desaprobaba la publicación de investigaciones de sus empleados. Para evadir esta prohibición, publicó su trabajo en secreto bajo el nombre de "Student". En consecuencia, la distribución t normalmente se llama distribución t de Student, o simplemente distribución t. Para derivar la ecuación de esta distribución, Gosset supone que las muestras se seleccionan de una población normal. Aunque esto parecería una suposición muy restrictiva, se puede mostrar que las poblaciones no normales que poseen distribuciones en forma casi de campana aún proporcionan valores de t que se aproximan muy de cerca a la distribución t.

La distribución t difiere de la de Z en que la varianza de t depende del tamaño de la muestra y siempre es mayor a uno. Unicamente cuando el tamaño de la muestra tiende a infinito las dos distribuciones serán las mismas.

Se acostumbra representar con el valor t por arriba del cual se encuentra un área igual a . Como la distribución t es simétrica alrededor de una media de cero, tenemos; es decir, el valor t que deja un área de  a la derecha y por tanto un área de  a la izquierda, es igual al valor t negativo que deja un área de  en la cola derecha de la distribución. Esto es, t_0.95 = -t_0.05, t_0.99=-t_0.01, etc.

Para encontrar los valores de t se utilizará la tabla de valores críticos de la distribución t del libro Probabilidad y Estadística para Ingenieros de los autores Walpole, Myers y Myers.

Ejemplo:

El valor t con  = 14 grados de libertad que deja un área de 0.025 a la izquierda, y por tanto un área de 0.975 a la derecha, es

t_0.975=-t_0.025 = -2.145

DISTRIBUCIÓN MUESTRAL DE DIFERENCIA DE PROPORCIONES

DIFERENCIA DE PROPORCIONES  El estadístico de prueba que permite contrastar frente a  a partir de dos muestras aleatorias e independientes es  siendo p la estimación de  obtenida del total de observaciones. Si se consideran las proporciones como medias y se aplica la prueba t utilizada para comparar medias poblacionales los resultados no son fiables ya que la estimación del error típico que realiza el programa no coincide con la del estadístico de prueba. Para resolver el problema con el programa SPSS se deberá cruzar la variable analizada con la que define los grupos (obtener la tabla de contingencia) y realizar el contraste de independencia Chi-cuadrado. El estadístico de prueba Chi-cuadrado se define:  y presenta una distribución Chi-cuadrado con (I-1)(J-1) grados de libertad. Las Eij se calculan multiplicando las frecuencias marginales y dividendo el producto por n. Estas Eij son estimaciones de las frecuencias absolutas que cabría esperar en cada casilla bajo el supuesto de que la proporción de éxitos es la obtenida a partir del total de observaciones muestrales sin considerar diferencias entre los dos grupos. La secuencia es: Analizar Estadísticos Descriptivos Tablas de contingencia En el cuadro de diálogo se indica la variable que se quiere contrastar (filas), la variable que define los dos grupos (columnas) y se selecciona la opción Chi-cuadrado en Estadísticos. EJEMPLO Con referencia a la encuesta Enctrans.sav se quiere comprobar si la proporción de alumnos con vehículo difiere significativamente entre los grupos definidos según el género. La hipótesis nula del contraste es ; siendo  la proporción poblacional de hombres con vehículo y  la proporción poblacional de mujeres con vehículo. Con la secuencia Analizar > Estadísticos Descriptivos > Tablas de contingencia se accede al cuadro de diálogo donde se indica que la variable a contrastar es Vehículo y que la variable de agrupación es el Género, y se selecciona la opción Chi-cuadrado en Estadísticos. Al aceptar se obtiene el siguiente cuadro de resultados. Si es cierto que la proporción de propietarios de vehículo es la misma en los dos grupos,  , la estimación de  es la proporción de propietarios de vehículo para el total de alumnos de la muestra, es decir, 39/114=0,3421. La frecuencia esperada de hombres con vehículo se obtendrá multiplicando esta proporción por el total de hombres en la muestra, o sea, 0,3421·54=18,5; y de la misma forma se obtendrá la frecuencia esperada de mujeres con vehículo: 0,3421·60=20,5 (veáse que estas frecuencias esperadas coinciden con las que cabría esperar en el caso de que las variables Género y Vehículo fueran independientes). El estadístico Chi-cuadrado toma el valor 0,998 y el nivel de significación crítico es 0,318, por lo tanto no se rechaza la hipótesis nula para los niveles de significación habituales y se puede aceptar que no hay diferencia entre la proporción de hombres y mujeres propietarios de vehículos.