estadistica inferencial 1: distribución Muestral de Proporciones

Las proporciones muestrales de tamaño $n \geq 30$ extraídas de una población con probabilidad de éxito 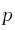, se ajustan a una distribución normal de parámetros:

$N\left(p, \sqrt{\frac{p\cdot(1-p)}{n}} \right)$

Se basa en la Aproximación de la Binomial a la Normal, por tanto, se considera una buena aproximación cuando se cumplan las condiciones $n \geq 30$ , $n\cdot p \geq 5$ y $n\cdot (1-p) \geq 5$
En la práctica la proporción de la población suele ser desconocida y se usa la proporción de la muestra $(\overline{p})$

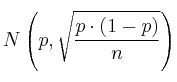
Una fábrica de pasteles fabrica, en su producción habitual, un $3 \%$ de pasteles defectuosos. Un cliente recibe un pedido de pasteles de la fábrica. Calcula la probabilidad de que encuentre más del $5 \%$ de pasteles defectuosos

SOLUCIÓN

Estamos tomando una muestra de tamaño , de una población donde la proporción de pasteles defectuosos es de . Podemos usar las Distribución Muestral de Proporciones, que se ajusta a una normal $N\left(p, \sqrt{\frac{p\cdot(1-p)}{n}} \right)$

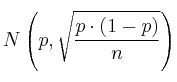
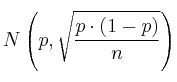
En nuestro ejemplo, si sustituimos los valores de 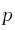y 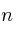y calculamos, sería

a) $P(\overline{p}>0.05) = P\left(Z>\frac{0.05-0.03}{0.0076}\right) = P(Z>2.63)=$
$=1 - P(Z \leq 2.63) = 1 - 0.9957 = \fbox{0.0043}$
Se ha tipificado la variable y se ha hecho uso de la tabla de la N(0,1)

estadistica inferencial 1

jueves, 13 de septiembre de 2018

distribución Muestral de Proporciones

SOLUCIÓN

No hay comentarios.:

Publicar un comentario